The Two-Layer Model

Gravity wave motion between immiscible, homogeneous, incompressible fluids can, provided any disturbances are small, be described by linear wave theory an a manner analogous to linear surface waves [67, 70, 71]. Consider two fluids of depth and with densities and , , separated by a sharp interface. Let the origin be at the interface with the x-coordinate horizontal and the z-coordinate vertically upwards. If the fluids are irrotational then they can be described in terms of a velocity potential such that the velocity is given by

Let the velocity potential be for and for . Now, the fluid velocity must satisfy the continuity equation so the velocity potential must satisfy the Laplace equation

We now consider the interface to be perturbed by a small amount where the perturbation is assumed to be a plane monochromatic wave with frequency , wavenumber k and amplitude a:

where a is the deformation amplitude and where it is understood that it is the real part of which is of interest. The following boundary conditions apply to the fluids.

1. The is no vertical motion at the bed,

    

2. Any surface motion produced by the internal waves is negligible and the surface can be considered as a solid boundary,

    

3. At the interface the horizontal velocity in both fluids must be the same as the . Using the linear approximation that all disturbances are small this can be applied at z=0,

    

4. At the interface the Bernoulli equation must be satisfied. If we assume that the waves are being driven solely by gravity and that the pressure difference across the interface is negligible then this can be expressed,

    

To solve the Laplace equation we look for wave solutions of the form

 

where A is an amplitude term and Z(z) describes the z-dependence of the solution. Substituting equation (6.10) into the Laplace equation gives

which has solution, subject to the boundary conditions equations (6.6) and (6.7),

 

Substituting equations (6.10) into the boundary conditions (6.8) and using the expressions for we find the amplitudes in terms of the deformation amplitude a:

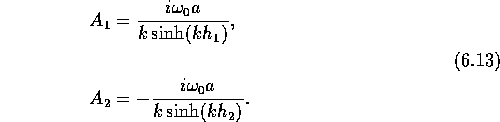
Substituting equations (6.10) into equation (6.9) and using the expressions for and gives the dispersion relation

If the interface is far from the bed and the free surface so that and this can be written in a form analogous to the dispersion relation for surface waves

 

where g' is the reduced gravity and is defined by

 

The velocity can be found by differentiating the velocity potential and taking the real part: