The boundary conditions in any fluid simulation are expressed either in terms
of the fluid velocity at the boundary or the velocity gradient at the
boundary. These are called Dirichlet and Neumann boundary conditions.
A method for imposing a Dirichlet boundary condition, for a fixed boundary,
to a
lattice Boltzmann fluid is devised by Noble et al.
[51, 50] for
a hexagonal and a square grid.
The boundary conditions developed by Noble et al. [51]
are for a
general velocity applied at a boundary
parallel to 
. The same approach can be
applied to any boundary but the details have still to be worked out
[51]. Here we consider the simplified situation of a non-slip
boundary parallel to . The velocity at the
boundary is to be zero. Consider a site at the `boundary' which has
fluid above it and a solid wall below it.
This is shown in figure 4-1
where the sites are labelled `fluid sites' is they are in the body of the fluid,
`boundary sites' if they are at the boundary and `wall sites' if they are
in the body of the boundary. The distribution functions approaching the
boundary site during the propagation stage are shown. These are the
distribution functions of the neighbouring sites at the previous time-step
.
Fluid is allowed
within the boundary sites but not the wall sites so the distribution
functions 
and 
are non-zero. Functions
and 
are zero and need to be specified so that the boundary condition
can be applied at the
site [51]. The boundary condition is 
:
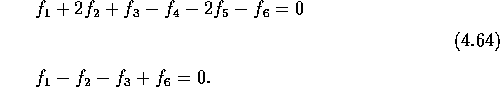
These can be solved for and , which become 
and 
respectively at the next time step. These are required in calculating the
new equilibrium distribution at the site.
Defining and in this way means that the density, the sum of
all the distribution functions, is also a calculated quantity.
This is different from the standard bounce back
boundary conditions where the density is a conserved quantity. Here
the density, and hence the pressure, at the boundary is calculated
by the algorithm to be correct for the desired boundary condition. This is
an important feature of the model as it is a necessary feature of the
boundary conditions [51, 52].
Other schemes have also been considered [53, 54, 55]. These are concerned with modelling particle suspensions where the boundary is frequently moving. Here we are only concerned with a stationary boundary.
