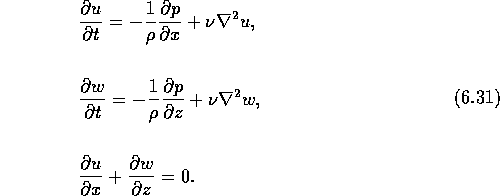
Consider internal wave motion between two viscous fluids separated by a sharp interface. This can be considered [74] in a manner similar to the treatment of surface waves [75, 76]. If the fluids are viscous then the equations of motion can be written:
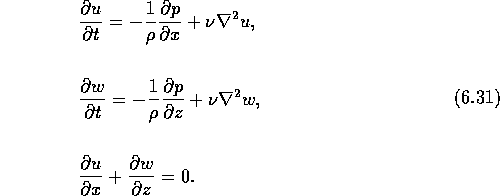
For the two-fluid system these have solutions [75, 74]
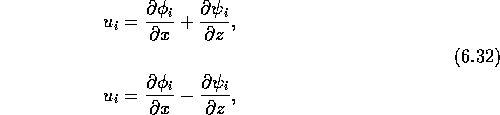
where
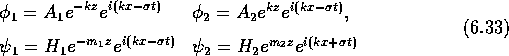
and
where 
is the viscosity of fluid i, i = 1, 2.
The boundary conditions at the interface are:
and 
across the interface
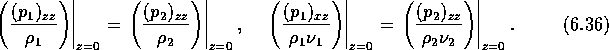
where p is given by the Bernoulli equation
For an infinite fluid
and 
can be eliminated by the interface boundary conditions
to give the `frequency' equation [74]
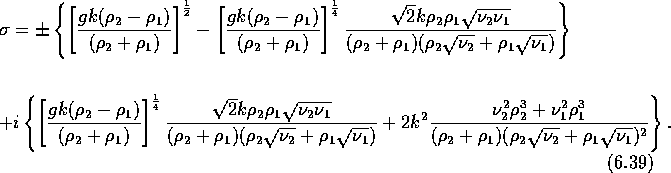
For a single fluid ( 
) this reduces to
which is the expression for the frequency and the proportional damping
of a surface wave [67].
Expressing 
in the form 
, where 
is the frequency of an inviscid
wave, and considering two fluids with the same viscosity
and with densities given by
a series expansion, in terms of 
, can be made for
[74]. To order 
the solution is [74]
and
The interfacial disturbance is now given by
where 
.
Thus the frequency (and hence also the celerity 
) is
reduced by an amount 
from the inviscid solution and the
wave amplitude a is replaced by a decaying exponential:
. In many situations and 
are small and of a similar size. In such situations the frequency
is only altered slightly from its inviscid value however the
damping term 
can produce a large effect when accumulated
over large times. As noted by Harrison [74] his solution is an
expansion in correct to order and also a series
expansion in k correct to order 
. This solution is in agreement
with the solution of Johns [77] which was found by considering
separate solutions inside and outside
the boundary layer, in a manner akin
to the treatment of the velocities in section 6.3.2, and
matching the two solutions. The solution of Johns [77] is only
to first-order in .
